It was a large part of my working life, prep work in construction involves measuring quantities needed it's impossible prepare accurate estimates without a working knowledge of Algebra
I actually used a bit of algebra last week at work, while discussing something with a coworker. I do have a technical job, so I am somewhat surprised that I don't use it more. On the other hand, I probably use the idea or concepts of algebra often. Much more than the "solve for x" math class stuff
Basic algebra, all the time. I need to put six widgets into each row. I have ten rows. How many total widgets do I need. I modify the plan, now I have 12 rows. As basic as it is, that is algebra.
The sad part of tist, I think that is very basic. Most Americans cannot do that.
I'm not a scientist or engineer, but I'm on the technical end of business.
I do a little "solve for X", but I'm waist-deep in graphing equations and statistics, even a little programming.
Calculus I rarely use the math, but the concepts of differential (first/second derivative) and integral (area under the curve) calculus are ridiculously valuable.
I do quite a bit of wood working as a hobby so I use algebra and geometry quite a bit for that.
I also just got back from a trip to Lowe's for mulch and some paint and supplies for repainting a guest room. I used basic algebra to figure out how much mulch and how much paint to buy.
You can use algebra to help you figure out how much better of value you get with a timed via session vs buying dances on a per song basis at the club. Of course taking the difference in mileage into consideration can be more complicated and if it is an extras club you can just throw the math out the window and enjoy your fun.
Almost 20 years after college I decided to go back for an MS degree. I had to take the GMAT which was relatively easy except for the Algebra/Quantitative Reasoning section. I found it wasn't anything like riding a bike, if you don't use it you lose it. B-school was a breeze after that.
I did okay on the quant section of the exam, but my percentile rank was lower than the other three sections. I think I studied as much for that one section of the GMAT as I had years before for the Series 7.
“ I use Calculus. I pay strippers to be their first derivative cause I like being tangent to their curves.”
Not me. I want to integrate with them. I like being in that area under their curves
I deal with fluid power concepts everyday and commonly use algebra to calculate force, pressure, flow, torque etc. But computerized engineering tools are making that less and less.
But I’ve kept all my math skills sharp over the years helping friend’s kids and now grandkids with their math homework. I was a math minor in college so I was the go to guy for math help.
I get several texts per week to help with a problem.
I don’t know of any TUSCL members admitting to being teachers but being exposed to the common core math that is being taught often doesn’t make a lot of sense to me. I’ve had math through Calculus 3, linear algebra, differential equations, and advanced statistics and find the way the problems are worded to be baffling like a non math person wrote it.
I don't use it in my accounting job. My great grandfather wrote an algebra textbook and made a lot of money from it, so it was very helpful he knew it.
Because of computers a whole lot of math can be applied, and we can do simulations. But you still have to be able to do the algebra and the calculus to solve things analytically to be able to put that into the computer first. And you need to be cognizant of the limits of algebra and calculus and to strategize around these limits.
SJG
Yeah doc what the FUCK is up with that, that accountants don't want to use Algebra. Like tax forms could probably be 10% as big if they'd just give you an algebraic expression. But no, it's all gotta be "subtract line 454954 from line 30489349 to get line 9304893".
If you have ever inserted multiple coins into coin operated device you have used algebra. Similarly, if you have ever verified that the cashier has given you correct change, or the ATM the correct number of 20s, you have used algebra. I realize these days the use of analog cash is dwindling, but I think most people on this list have done these things.
Polynomial Math comes up in a lot of things, as does Rational Polynomial Math, and then Matrix Math, and then Transforms like the Fourier and like Convolution, and there are a lot of other things as well.
SJG
Non-Linear Dynamics or "Chaos Theory" is becoming very fruitful, and this is because of computers, which need to use to even be able to visualize it. And likewise with Complexity Theory, and with all that is coming out of the Santa Fe Institute.
SJG
The guy with about seven screen names on two strip club message boards, when he's only seen two vaginas in his life, his mother's and his sister's, has no standing to opine on that.
Nor anything mathematical. There's a reason you log on right after a school bus might drop a student off at home every day.
I used algebra frequently when I was working. Now algebra comes in handy for creating financial models and planning my financial future. If 3 strippers see me OTC twice a week, how long until I go broke?
Q. Why is a stripper like an algebra textbook?
A. They both have a lot of problems.
All the time, even on my weekend projects. I'm stainjng two 8x4x4 posts with two coats, whats the surface area. I'm filling two 6 gal planters, less the post footing, with concrete. What's the volume? Etc.
A lot of math gets used to explore hypotheticals and to make predictions:
General Quadratic Solution
[view link]
In the biography of Elon Musk he had gone to Moscow seeking to buy two Vostok Boosters. He did not like the price the Russians were holding out for.
So he did his own analysis using a spread sheet program. He knew that communications satellites continue to get smaller. So what does that mean for the size of booster needed to launch one into orbit? And then what does that say about the cost to make the booster. So sitting in an airport lobby anxious to leave Moscow, he decided to start Space-X and to make his own booster.
If you want to design something you will often need to use algebra to work back from the targeted final result to the original input parameters. And you need to know when algebra cannot do this and when you have to resort to using computers to apply numerical methods.
And then for 30 years now we have been using Statistical Quality Control, and this is most effective when you have computers taking input and monitoring production flows. But you still have to understand the math yourself to make this work.
And likewise for 30 years we have been using Data Driven Manufacturing, when machines route the necessary resources as best to accomplish the goals.
And so we used to have WHIP Systems (Work in Progress). And then it was Manufacturing Execution Systems, and now the more extensive Enterprise Resource Planning Systems.
And especially when there are transportation networks involved and when there is an attempt to minimize costs of big inventories is materials, you have these computer optimization problems. The machines will do the work operationally, but you still have to do the math yourself to set it up.
And then even considering something like fuel choices for rocket motors versus air breathing motors, you have to use the Periodic Table of Elements to figure out mass ratios for stochiometric reactions.
Having access to programmable calculators and computers encourages one to try and mathematically model more things. They computer lets you go beyond what would be possible to do with hand calculations, but you still have to set the math up yourself on paper, to be able to do this.
Now sure, Archie Bunker, in front of his television set, and Homer Simpson, do not do this. I really comes down to what you want.
I went to school with a lot of people who said, "You'll never need to know this out in the real world."
Well it depends on what you want, if you want to live by just going with the flow and by people pleasing, I guess it can be like that.
But not everyone wants that.
SJG
X - Burning House of Love (Live at Farm Aid 1985)
[view link]
I used algebra pretty regularly in my professional life. I still keep my hand in it mainly by solving financial scenarios, and things like how to avoid a speeding ticket with a blank screen digital speed read, but a workable analog tachometer on a Corvette. (Hint, the 2002 to 2004 Z06 at 60mph would be showing 1500 rpm in 6th gear. Keep 1600 or less in a 65 zone, 1700 or less in a 70 zone, and you'll be OK.)
A lot of math gets used in financial calculations, like Internal Rate of Return and Net Present Value, for annuities and amortized loans, and then for returns on investments. People who fly airplanes have to figure out center of gravity and inertial moment. And these are serious matters!
I high school I was electrolysising water to get the hydrogen for balloons, and I had to compute the maximum weight based on volume, and also factoring in air pressure and temperature. In school we did something like that with a D size dry cell. I was doing it with a car battery charger. So how fast could I make hydrogen?
The limits of most solid state electronics is found in thermal resistance and temperature rise.
A lot of algebra, as opposed to just plugging in numbers, gets used when you are trying to figure out the optimum way of doing something, according to some criterion.
SJG
Computers can plug in the numbers and do all of the numerics. But because of this there is more reason to use algebra and calculus. You have to back solve things, and often you will want to know when the first derivative is zero and the sign of the second derivative.
I remember when I got my first scientific calculator, trig and exponentials, you can figure out feasibility of all sorts of things, and deal with all the inevitable units conversions. Having these computing tools leads to a vast increase in the amount of symbolic math.
SJG
My father taught trigonometry in high school sixty year ago. I've never had the faintest idea what that would be used for, and I don't hear about any young people taking it in high school these days. Is that something that was dropped from the high school curriculum because it has little practical application or were pocket calculators or computers developed that could do that, so people no longer need to learn it?
I’ve also heard that only about half of high school geometry courses still teach formal two-column proofs.
Granted, that’s a skill one will most likely never use again in real life, but it did help develop critical thinking skills - at least I think so
For example if you want to measure how high a model rocket is going you can sight from the ground and then multiply the tangent of the angle by the baseline. If you want a better calculation you can use two spotter and use trigonometry to figure out the altitude and also where the apogee was occurring relative to the launch site.
And then say you want to know AC current power factor, because that tells you how much extra current a load is drawing relative to its power rating. So a motor represents and inductive load and so the voltage will lead the current and so the power factor is the cosine of the angle between them.
And then which figuring things about about longitude and latitude, spherical coordinates, it will always require trigonometry.
How much arc does a Foucault's Pendulum go through in 24 hours?
[view link].
And then in the 8th grade I read a book about the design of jet aircraft engines. Besides exposing me to thermo dynamics, it also exposed me to much more trigonometry because the turbine rotos have blades at a given angle. Usually the angles can be adjusted, so what do compressor turbines do?
SJG
How to cut pieces of cloth to make a spherical parachute.
Figuring the great circle distance between to cities by longitude and latitude.
Strength of sun light on a photovoltaic cell when it is not directly facing the sun.
All require trigonometry.
SJG
I’m guessing the OP knows there are real life examples of necessary uses for these sets of math skills. The point is that the US educational system pushes students to learn everything to a high level in each subject, when if given some extra thought and consideration it would be more efficient to teach those skills mostly to the students inclined to need or want to use those skllls. There’s are many of us in the $350k + income bracket who never had to apply those math skills after formal schooling.
Well, I've been reading about stuff like that, at the end of this thread:
[view link]
Well, generally questioning people about stuff in job applications is okay so long as it is about stuff which is relevant to the job description.
As far as college applications, I don't think schools make that much use of SAT scores anyway. And of high school grades, it is only some schools which are really that hard to get into.
In our Community Colleges there are remedial math programs which are good and they will test you to see if you should be in this.
But the basic idea is that such things do separate the students and are very correlated to socio-economic status, and that this in turn has a strong correlation to race.
I think what it comes down to is what social environment the child has grown up in. Much of the academic things will have no relevance to the parents. And you see on this thread that math doesn't mean much to a lot of the adults who like strip clubs.
These are not easy issues. On the above thread I am talking about the Gifted Movement, and then also about the critics of the Gifted Movement. They object to school tracking and to even ability grouping. I am reading them because I want to understand them, and I talk about some of my own experiences.
Some private schools and some public schools are impacted, far more people who want to be there but can't.
But most colleges are not that hard to get into.
Generally standardized tests and things presented as IQ tests are largely cultural affinity tests and they are socioeconomically biased and racially biased.
Tough issues.
SJG
SJG - your comment about old hand held calculators made me think back.
I don’t know your age, but I’ll date myself here. In my high school physics class we could not use a calculator until we demonstrated proficiency with a slide rule. No one had calculators but there were two HP calculators available for the entire class to share. And if you remember the original HP calculators used RPN - Reverse Polish Notation. Kind of difficult to use.
I talked by parents into getting me a TI scientific notation calculator which I used for high school physics and all of college. It was about $125 which was expensive back then.
All the time. I don't use calculus nearly as much as I thought I would when I learned it, but I have the kind of mind that can work the equations 45 years later.
—>“I don't hear about any young people taking it in high school these days. Is that something that was dropped from the high school curriculum “
I remember trig was hugely required in pre-cal and geometry class. And this was the late 2000s. I think high school students still have to study it. 🤔
Computer programmer, so I use it a lot. For too often I use it to simplify subroutines and functions where the original developer didn't simplify equations, and instead relied on compilers to reduce the equations. While compilers are able to simplify non-complex expressions, when they are buried two or 3 levels deep not so much, or in cases when one calculation cancels out part of another.
I have been retired now for a bit so actually writing out an equation and solving it is rare these days I was an EEvmajor in college so I had the whole gambit of math (algebra, geometry, trig, calculus, differential Equations, etc). Did I use all of what I learned in a applied way? No, only bits here and there. But the breath of my math education has enhanced my understanding of how things work. I don’t retreat the math I was taught one bit
Several times a week around the house. Mostly I use it on things like cooking/scaling recipes up or down, or light projects home improvement/repair projects. At work its hit or miss, some weeks its all the time with project planning or vendor negotiations, capacity planning and the like is heavy on the basic math. Some weeks its more complex math. I think Heaving said it best earlier in the thread, learning math hasn't been about doing the calculations for quite some time now. It's about understanding the concepts and principles, how to solve problems.
I know strippers aren't generally regarded as being the most intellectual, but just the other day I was at a club that did two for one dances. The girl didn't want to continue dancing for me after the first two songs, because she "can't never figure out how much" so she stopped and insisted on being paid for the two for one instead of continuing for another likely 3-4 songs and finishing what she started. So she lost out on $60-80 plus a tip because she couldn't do what could be considered basic algebra. I went and got dances with another girl about 20 minutes later. The first girl came over again after, realizing that she lost money, and it lead to a conversation about how to "figure out how much" where she explained that not only can't she count dances after starting with a 2-4-1, she also can't multiply by 25. She just memorized the cost of up to six songs and when customers get that far she stops and makes them pay then. She tells them its because she's worried about getting stiffed, but its really because she can't multiply. I spent 15 minutes explaining to this girl that in the two for one situation, she can just start counting songs after the first one ends. She eventually realized on her own that she could also "just minus one" if she counted them all. I tried to use what I can only explain as a quarters analogy to teach her to do the math, but she couldn't see the link. She could tell me 10 quarters was two dollars and fifty cents and about 3 other similar scenarios she quickly got right, but couldn't relate that to whole dollars. I think she just couldn't focus because she was so happy she could now keep going after the 2-4-1. We tested her on the next one, she stayed with me for 5 total songs. She was so happy that she could determine that I owed her $100 the she absolutely refused to take anything from me. She literally stuffed my money in my pants when I tried to pay her, and I was trying to pay her a fair bit more since she went above and beyond. She also wants to come over and thank me again "with no fuckin math, no cap" whatever the fuck that means. I guess she's lost a lot of dances stopping after two for one. Moral of the story is, pay attention in math class. Or you could wind up sucking dick to learn it later.
I use it daily when recording my meals, so I can estimate timing of my next bowel movement...
try to avoid having to go when I'm expecting to be stuck in traffic!
SJG uses it.
“If I give this guy a hand job behind the library he will give me 10 aluminum cans. If I give him a blow job he will give me 20 aluminum cans, and if his friend gets to watch he will give me 3 aluminum cans. No matter how many cans I get it will not be enough for a visit to Mamisan.”
Motorhead, I also had to learn in school several times, to use slide rules. And this meant for log and trig, and how to interpolate for an extra digit, and going either direction.
I posted a thread years back now about HP Calculators and RPN. I love it. You can still get it in the HP-Prime, now I think version 2, and I've seen real good online discounts.
Heavings, if you want to make the computer solve something, you first have to set up the equations the right way yourself. This means that you have to do the symbolic math yourself. Because computers will do the numerics, you end up doing more algebra, trig, and calculus yourself because you will be able to count on the computer more.
And people use as much math as they want to. Sure, some people become like Archie Bunker and Homer Simpson. But not all of us do that.
About trigonometry, one place you would use it is in surveying. If you want accuracy you need to do it in triangles. Say you have a steel tape and you measure the distance between two points you have marked. Say it is about 100'. Then you mark a 3rd point and measure the two inside angles.
There are various theorems about what it takes to define a triangle, such as Angle Side Angle.
[view link]
So you measure the two inside angles and you use that with your steel tape measurement and you now know the other two sides and the other angle.
[view link]
Law of Sines gives you the other two distances:
[view link]
And so if you can measure and compute with some good accuracy, you can continue marking other points and scale up to well beyond your original 100' steel tape distance.
Algebra and Trigonometry will do this for you.
And as far as people learning algebra in high school, of course they do, and sometimes even 2 years earlier now in the Gifted Movement, I read.
And at our community colleges they will have remedial math programs because you will need to know this stuff to take the college level math.
SJG
X- Live At The Whisky A Go Go
[view link]
Really I think if you want to build something, want to design it, you will have some equations which govern its behavior. But if you want to change what is known and what is unknown, then you have to use algebra.
Early in high school a teacher gave me an article which had some equations for designing multi vibrator circuits.
I looked and I solved them several different ways, making different things the unknown. Then I wrote a computer program which would let you select which of the four versions you wanted to plug the numbers into.
Getting a bag of high frequency transistors I had fun making battery powered broadcast television jammers.
Making a geodesic dome model, out of plastic drinking straws and fishing line.
The geodesic dome is an interpenetration of an icosahedron (20 sides) and a dodecahedron (12 sides)
[view link]
And so not every place on the dome is the same:
[view link]
Corners of 5 and corners of 6.
And then once you have this figured out, it comes down to how many cycles per panel.
[view link]
How well it works depends on accurate design and cutting of the strut lengths.
For mine I did figure it on on paper and then measure carefully with a metric ruler and cut.
For mine there were three lengths of straws, but it took me a while to figure all of this out, and it did use trigonometry.
Some stuff you can use theorem of Pythagoras, if you have a guaranteed right angle. And most of the trig identities somehow are derived from this. But when things are intended to be strong, they have to work by tensile strength, not by gusseting corners. And this was always one of Fuller's main points. So you have to use trig and cut your struts to the right length.
One I had a scientific calculator that made it possible to consider endless hypotheticals and feasibility studies for all manner of things.
Motorhead, about the HP RPN Calculators, and I had gotten the Polish Mathematicians book that they got the idea for RPN from and I read it. And then there were differences when they went to HP-48 and RPL. And I think now they have scaled it back with the HP-Prime.
[view link]
SJG
Hope You're Feeling Better ~ Santana
[view link]
Algebra Problem
Given the menu and nutritional info at Taco Bell, and assuming no food allergies, what is the minimum order required to generate enough caca to plug a standard North American toilet? Omit any hot sauce that could interfere with normal digestive process.
^^^ Very true!
And especially if you are trying to do something in a different way than what is printed in books, then you need to use algebra to set up the equations, and often calculus too. Trigonometry comes up in mechanical and structural things, but also in things which are time harmonic, and so having a phase angle.
HP RPN Calculators
[view link]
HP-PRIME
$123.00
[view link]
RPN and 33 to 34 decimal digits, so it seems to do 128 bit floating point!
SJG
Vanilla Fudge
[view link]
HP-48, 49, 50, and 51 had this compounded variable typing, like an object oriented approach to a mathematics library.
"
So in the stack you can enter a real number. You can also use the hash tag to make it binary. Leading 0 to make it Octal, leading with Ox to make it hexadecimal. It shows this on the front face of the model 28, that it is 'objects' which go on the stack. Lead with double quotes for strings, and single quotes for variables, parentheses for complex, square braces for vectors and double square braces for a matrix.
"
But do you really want all that in a calculator?
[view link]
And then to get back to our OP, is he really asking how much you use algebra, or just how much math you use?
A powerful handheld calculator, or a computer program with the better display, keyboard, and mass storage, lets you do all sorts of math for every hypothetical you can imagine.
But with specifically algebra, when you have equations describing something and you want to change what variables are know and which are unknown, then you do need to use algebra, and usually this is still not done by machines.
SJG
X - Burning House of Love
[view link]
Long division is hard. I think some people never learn, and beyond a point it is worthless to try in school to make them learn. It is tedious, and not everyone really wants to learn.
With the calculators today, not sure if people do learn. And like Motorhead talked about, we also learned how to do math on slide rules.
I posted on another thread about a time that a teacher divided us into math groups with a quiz to see if we could multiply 3 digit numbers. What the top group got to do was really fun, Set Theory and using that to develop Geometry.
I think many people have a bad experience with math just because of the way it was taught to them. It convinced them to give up trying to learn more. This should be changed.
SJG
Using algebra, ball point pen on paper, because too easy to get refill tea spilled into a laptop at Viet Coffee:
[view link]
and about Calculators
[view link]
SJG
X-Burning House of Love
[view link]
I've talked here about the ideas of the gifted movement.
[view link]
And I've also talked about some of the ideas from those who are opposed to the Gifted Movement and who are opposed to school tracking.
It is difficult to teach mathematics. And to understand the physical sciences, and hot just relate to it through buzz words, you need to understand some complex mathematical relationships.
But here adults post and you find some with a very negative and dismissive view of mathematics.
And then I can say that in the industrial work place, you cannot talk much about things which revolve around mathematics. And then even with groups of people who have completed math intensive degrees, in the work place they turn into Frat Boys. All they care about is looking cool and the newest cool graphics computer software. They don't want to really understand or commit to building the tools that are needed, or to using the wisely. They have lost the power for individual thought.
So some critics of the gifted movement want to do away with school tracking, and even some in the gifted movement think this would be better.
But fair or not, hard to get people interested in mathematics unless it is some carrot and stick situation. I think actually that the parents are worse than the kids in having horrible attitudes.
They say that for gifted kids the best teachers are those who have committed to and practice life long learning. But I say these are the best teachers for everyone, and that you need this in the industrial work place as well.
SJG
Frampton w/ Bob Mayo
[view link]
FWIW, last night I just used algebra to figure something out. It is something I had worked out when in jr high school. It is not obvious and you kind of can't do it by working straight to a solution. You have to just recognize the key relations and write the equations.
It is about making a conical section to flare from one diameter to another. And it has a span, so you use Thm of Pythagoras to figure the actual length of the conical section. So you want then the radii of two drawn concentric arcs, as well as the angle they span.
So your write out the relations and then it solves very easy by subsitution.
And this is exactly the kind of analysis you would have to do to design women's skirts and dresses with a flare:
[view link]
SJG
every day. Cross multiplication my most used algebra technique. Followed by Orders of Operations. Algebra has to be the most necessary common math used by most people of the world.
So I talked above about how to design a conical flare, 3 unknows, and how this would be the same as for a woman's flaring skirt.
Might not have a protractor large enough to do a good job measuring the angle. BUt with a roofing square held at a radius and square with the first radius, you can take the sine of the angle.
[view link]
A right angle from a radius, and the sine of the angle multiplied by the radius is the height of the perpendicular. With a 600mm roofers square, that is far more accurate than what you can do with most protractors.
SJG
whodey and jackslash covered the ITC and OTC sides of it pretty well. I probably did some low tech form of it when I'd work through which clubs to see on what days on a business trip.
To riff off whodey's take, it sounds like his mileage idea was more of a maximization function. Example using fish here at [view link]. Swap in whatever you like for the tetras and headstanders. You want to get fancier then welcome to calc and I'll see myself out.
Yeah want to analyze all the issues for the best ways to measure resistance of RTDs, and usually be a bridge. This will mean algebra at a minimum.
[view link][view link]
SJG
The Rolling Stones - Gimme Shelter - 2013 School of Rock AllStars Team 4
[view link]
So I thought the standard was 500 ohms. But they say it is sometimes 1000 ohms, and more likely 100 ohms.
And they have resistance versus temperature tables. The Euro one is seen as the standard. Don't know how linear it is.
Say you wanted to run from 100 deg C down to minus 190 deg C (about liquid oxygen)
So if you drive the bridge with an ideal voltage source, zero internal resistance, and you measure with an ideal volt meter, infinite internal resistance, then you want the voltage transfer function for the bridge.
Here is the European table in 1 deg increments. Goes down to minus 200 and then to very hot.
3 pages
I think you need to find out what kind of curve fitting really works well on this.
[view link]
100 ohms at 0 deg C.
18.52 ohms at -200 deg c
80.31 ohms at -50 deg c
109.73 ohms at 25 deg c
138.51 ohms at 100 deg c
SJG
The Rolling Stones - Gimme Shelter - 2013 School of Rock AllStars Team 4
[view link]
PEMDAS? How about posting a link to these questions they ask on Facebook.
Here talking about 2, 3, and 4 wire RTDs.
[view link]
And here is the solution for the bridge circuit.
<img src="[view link]">
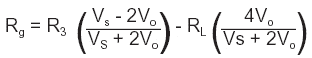
But I am still trying to understand this before doing the algebra.
SJG
The Rolling Stones - Gimme Shelter - 2013 School of Rock AllStars Team 4
[view link]
But better to show generosity and get a front room make out session going, then and only then invite her to the back room, and then take her to bed and keep seeing her regularly, and avoid places where you have to tip bouncers because that makes them into pimps.
SJG
[view link][view link]
The Rolling Stones - Gimme Shelter - 2013 School of Rock AllStars Team 4
[view link]
Reading a Calculus book and it talked about Taylor Series and all manner of power series.
And then is how you get irrational numbers.
A conversation with a friend, and organ player. I explained about how temper tuning, done perfectly requires a semi-tone to be 12th root of two above the note before it.
We talked about tone wheel organs and I explained that those have a rotational cycle, so you can just approximate the interval. ANd the same is so for digital synths which may have a very high clock speed, but still can only approximate it.
He was not used to the idea of irrational numbers. So I explained about logarithms and that this is how you get the number, but if you have to make the log table book youself, then you use a power series.
It brings back to mind a long in class argument I had with a jr high school math teacher. She was explaining about the number PI and how it was irrational.
I was saying that it was not. The circumference and diameter of a circle were definite values, and so if you divide them you get either a termination or repeating decimal.
She was sure she was right. And now years later I also know that she was and I feel foolish about all of that.
But in class her arguments were not very strong. She did not have a geometrical construction or a power series proof for what the value of PI was. She was doing it from a king of empirical argument, but this really fed my argument.
Irrational number come not just from division. It has to be an endless series of divisions added together. And for Calculus to work you need to have this kind of a number space.
SJG
Reflecting more on the classroom debate I had in jr high school. The teacher did not have strong arguments for PI being irrational. It was just a claim she made. She had no explanation for how the value of PI was found, or about power series. She just said it was the ration of the circumference to the diameter.
Well that way, I was right, it had to be either terminating or repeating, hence rational. You can't get an irrational number by division. You can only get them by a sum of quotients.
What Is Pi, and How Did It Originate?
[view link].)
Additionally, pi shows up often unexpectedly in many mathematical situations. For example, the sum of the infinite series
1 + 1/4 + 1/9 + 1/16 + 1/25 + ... + 1/n2 + ... is π2/6
^ I do not know where this came from or that it works or why.
[view link]
Around 250 BC, the Greek mathematician Archimedes created an algorithm to approximate π with arbitrary accuracy.
There are several proofs that π is irrational; they generally require calculus and rely on the reductio ad absurdum technique.
Proof_that_%CF%80_is_irrational
[view link]
SJG
Pleaser
[view link][view link][view link]
The Kinks - Till the End of the Day (1965) ( like the images of the neat old cars )
[view link]
THE BYRDS Greatest Hits - The Best Of THE BYRDS | HD/HQ
[view link]
Yardbirds Anderson Theatre 1968
[view link]
Shirley Manson
[view link]
Algebra also helps teenagers think more logically and promotes critical thinking skills.
When I studied calculus in high school there were no calculators and I found slide rules to be very difficult. I’m 1969 my wife and I were at a closing, buying property. The lawyer had a calculated on his desk. It was about 3/4 of an inch in thickness and he proudly demonstrated that it could do all 4 functions. And he proclaimed it only cost $325.
About 50 years later I told his daughter that story and she started laughing. Apparently he made such a big deal about it his family had it encased in a block of lucite.
Yes, thinking logically and critical thinking skills.
In lucite?
Today you can get financial calculators which do all the amortized loan stuff. But you can do it manually too.
SJG
Pleaser
[view link]
Shirley Manson
[view link]
So thinking more about irrational numbers. There are far more of them than the rational numbers. And you can't get them by doing division. You get them by and endless series of sums of divisions.
The ways that computing machines do math is not really compatible with this. They have a particular assigned precision and they don't distinguish between terminating decimal, repeating decimal, and irrational.
And as the ones you can get from division are terminating and repeating. These are exact results too, unlimited precision.
So do treat these in computing machines you need to be doing the division in such a way that you recognize the repeating portion, and then with enough digits to cover the two input numbers.
And then terminating versus repeating varies with number base. 1/7 done decimal is repeating. But change it to base 7, 1/10 is terminating.
Do you have to do the math base 10? Use that old BCD system from the finance sector, one 4 bit nibble for each decimal digit.
The one which probably goes the furthest now if probably Mathematica. But that is probably not the one which does the most practical math.
If my jr high school teacher had a better power series type argument for the value of PI, I would not have challenged her.
SJG
PBS NewsHour live episode, May 18, 2022
[view link]
So thinking more about irrational numbers. Talking to that friend about 12th root of 2 in tempertuned music. Today you would just get that off of a calculator. If you did not have a calculator you would do it from a table of logarithms. But for all the stuff, how many table would you need?
One for log, any base, will do you for logs and exponentials.
For trig, if you have sine or cosine for 90 deg, then that covers you for the other, and for the inverse, for 360 deg. It covers you for tangent too.
But how about inverse tangent, do you need another table?
Well having retrieved my Raymond Serway Physics book for the guy who had borrowed it, I see it says,
csc^2(theta) = 1 + cot^2(theta)
and of course csc= 1/sin and cot = 1/tan.
I think you could figure out the above from thm of pythagoras.
So say you want Arctan(10).
So you want 0.1 = 1/tan(theta)
or 0.01 = sqr(1/tan(theta))
So 1.01 = csc^2(theta)
sqrt(1.01) = csc(theta)
sin(theta) = 1/sqrt(1.01)
So theta will be an angle almost 90 deg.
So one log and one trig table can do it all.
I kind of remember in discussions of Intel's original 8087 coprocessor design, of transendentals it had just a couple, and I think one was for cotangent.
So one trig, one log does it all!
Maybe you need something else if you need hyperbolics.
Want now to see:
[view link]
Only book I've seen which separates this stuff out. Now I see that there are others too.
Calculus : early transcendentals / James Stewart (2012 for 7th edition)
Stewart, James, 1941-
SJG
Deep Purple - Hush - 2013 School of Rock AllStars Team 4
[view link]
Pleaser 10" lots of colors
[view link]
I Use pythagorean’s theorem AT LEAST once a week…
It sounds like im joking but i work in construction and its the fastest, most accurate way to find true square for a layout. Also occasionally to do arches or a rounded wall or patio (or to figure out quantities for them) theres a few different equations you need to know, segmental arches being the trickiest. Great strip club banter too by the way 🤣
I also use proportions pretty frequently to figure out two related quantities but with incomplete information. Very useful.
In the club i use a different type of proportions to find what im looking for - the waist to hip and boob to stomach ratios being key to determining a dancers tip quantity lol
Anyone got an equation for this?
The history of the calculus and its conceptual development : (The concepts of the calculus) / with a foreword by Richard Courant
Concepts of the calculus.
Boyer, Carl B. (Carl Benjamin), 1906-1976.
Books & Journals | Dover | [1959]
So he talks about the paradoxes of Zeno. Like say in a time interval, you move half of the distance between yourself and a fixed point. And then in the next interval, half of what remained, etc.
When to you finally get to the point?
This had come up in a conversation with someone who was ticket for not coming to a complete stop at a stop sign. How slow is slow enough to be stopped?
But Boyer speaks of another Zeno formulation. Say Achilles runs a race with a tortoise and Achilles runs twice as fast as the tortoise, and so we give the tortoise a lead.
So when does Achilles catch up with the tortoise?
Well for the ancients they were not really accustomed to finding limits for infinite series.
For me, I would set it up as an algebra problem
Say Achilles runs at velocity Va.
The lead given the tortoise is Lt.
So the time when Achilles catches up with the tortoise will be Tc. And the distance Achilles has run will be Da.
Da = Tc * Va
Da = Lt + Tc * Va /2
So then we can eliminate Da:
Tc * Va = Lt + Tc * Va /2
So then:
Tc * Va - Tc * Va/2 = Lt
Tc * (Va -Va/2) =
Tc * Va/2 = Lt
So say the velocity of Achilles is 10 ft/sec, then the velocity of the Tortoise is 5 ft /sec.
So say the lead we gave the Tortoise was 100 ft.
So Tc = 2 * Lt / Va
So Tc = 2 * 100 / 10 = 20 seconds.
So Achilles will have run 200 ft
The Tortoise will have run 100 ft and then be 200 feet from the starting line.
Now this kind of approach does not get into convergence of infinite series or into calculus. It just uses algebra. But I guess it is a way of using algebra that has developed in a where our under standing of time and motion has been shaped by calculus. And I have learned from from years in school, having to do homework problems with word problems like this, and also by regularly solving similar kinds of problems on my own. You cut through the confusion by defining variables and laying out the relations.
SJG
102 comments